Consider an infinite triangle made up of layers. Let’s number the layers, starting from one, from the top of the triangle (from top to bottom). The kk-th layer of the triangle contains kk points, numbered from left to right. Each point of an infinite triangle is described by a pair of numbers (r,c)(r,c) (1≤c≤r1≤c≤r), where rr is the number of the layer, and cc is the number of the point in the layer. From each point (r,c)(r,c) there are two directed edges to the points (r+1,c)(r+1,c) and (r+1,c+1)(r+1,c+1), but only one of the edges is activated. If r+cr+c is even, then the edge to the point (r+1,c)(r+1,c) is activated, otherwise the edge to the point (r+1,c+1)(r+1,c+1) is activated. Look at the picture for a better understanding.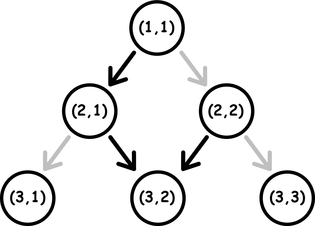
Activated edges are colored in black. Non-activated edges are colored in gray.
From the point (r1,c1)(r1,c1) it is possible to reach the point (r2,c2)(r2,c2), if there is a path between them only from activated edges. For example, in the picture above, there is a path from (1,1)(1,1) to (3,2)(3,2), but there is no path from (2,1)(2,1) to (1,1)(1,1).
Initially, you are at the point (1,1)(1,1). For each turn, you can:
- Replace activated edge for point (r,c)(r,c). That is if the edge to the point (r+1,c)(r+1,c) is activated, then instead of it, the edge to the point (r+1,c+1)(r+1,c+1) becomes activated, otherwise if the edge to the point (r+1,c+1)(r+1,c+1), then instead if it, the edge to the point (r+1,c)(r+1,c) becomes activated. This action increases the cost of the path by 11;
- Move from the current point to another by following the activated edge. This action does not increase the cost of the path.
You are given a sequence of nn points of an infinite triangle (r1,c1),(r2,c2),…,(rn,cn)(r1,c1),(r2,c2),…,(rn,cn). Find the minimum cost path from (1,1)(1,1), passing through all nn points in arbitrary order.Input
The first line contains one integer tt (1≤t≤1041≤t≤104) is the number of test cases. Then tt test cases follow.
Each test case begins with a line containing one integer nn (1≤n≤2⋅1051≤n≤2⋅105) is the number of points to visit.
The second line contains nn numbers r1,r2,…,rnr1,r2,…,rn (1≤ri≤1091≤ri≤109), where riri is the number of the layer in which ii-th point is located.
The third line contains nn numbers c1,c2,…,cnc1,c2,…,cn (1≤ci≤ri1≤ci≤ri), where cici is the number of the ii-th point in the riri layer.
It is guaranteed that all nn points are distinct.
It is guaranteed that there is always at least one way to traverse all nn points.
It is guaranteed that the sum of nn over all test cases does not exceed 2⋅1052⋅105.Output
For each test case, output the minimum cost of a path passing through all points in the corresponding test case.ExampleinputCopy
4 3 1 4 2 1 3 1 2 2 4 2 3 2 1 1000000000 1 1000000000 4 3 10 5 8 2 5 2 4
outputCopy
0 1 999999999 2
Solution : Coming Soon